-SKplanet Tacademy의 컴퓨터 알고리즘 초급 강의를 듣고 정리한 내용입니다-
https://tacademy.skplanet.com/live/player/onlineLectureDetail.action?seq=83
컴퓨터 알고리즘 초급 | T아카데미 온라인강의
컴퓨터 알고리즘은 성공적인 프로그래밍을 위한 필수적인 과목입니다. 본 과정에서는 컴퓨터 알고리즘의 정의에 대해 학습하고 필요성을 인식하며 이에 대한 기본내용을 학습합니다. 또..
tacademy.skplanet.com
합병정렬
- 합병을 이용한 정렬 알고리즘
- 이미 정렬되어 있는 2개의 배열을 비교하여 작은 값을 새로운 배열에 넣음
- 수행시간 O(nlgn)
<합병정렬 예제>
| Merge | A | B | C | ||||||||||||||||
| Step 0 | 1 | 5 | 6 | 8 | 2 | 4 | 7 | 9 | 1 | ||||||||||
| Step 1 | 5 | 6 | 8 | 2 | 4 | 7 | 9 | 1 | 2 | ||||||||||
| Step 2 | 5 | 6 | 8 | 4 | 7 | 9 | 1 | 2 | 4 | ||||||||||
| Step 3 | 5 | 6 | 8 | 7 | 9 | 1 | 2 | 4 | 5 | ||||||||||
| Step 4 | 6 | 8 | 7 | 9 | 1 | 2 | 4 | 5 | 6 | ||||||||||
| Step 5 | 8 | 7 | 9 | 1 | 2 | 4 | 5 | 6 | 7 | ||||||||||
| Step 6 | 8 | 9 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | ||||||||||
| Step 7 | 9 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| Step 8 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||||
A divide-and-conquer approach
- 크기가 커서 풀기 어려운 하나의 문제를 크기가 작아서 풀기 쉬운 여러 개의 문제로 바꾸어서 푸는 방법
Divide
- n keys를 두 개의 n/2 keys로 나눈다.
Conquer
- 합병정렬을 사용해서 두 개의 배열을 정렬한다.
합병정렬

한 개가 될 때까지 쪼갠다. -> 그리고 합병정렬
합병정렬 슈도코드
MERGE-SORT(A,p,r)
if p<r
q = [(p+r)/2]
MERGE-SORT(A,p,q)
MERGE-SORT(A,q+1,r)
MERGE(A,p,q,r)
[A : n개의 숫자가 들어있는 배열]
[p : 그 배열의 첫 번째 수]
[r : 그 배열의 마지막 수]
힙 정렬
- 힙 구조의 특성을 이용한 정렬
- 수행시간은 O(nlgn)
- 삽입정렬과 동일한 제자리 정렬
힙의 형태
- 완전 이진 트리에 가까운 형태
- 이진 트리는 각 노드의 자식 수가 2이하인 경우
- 완전 이진 트리는 Root 노드부터 Leaf 노드까지 빠짐없이 채워져 있는 트리
힙 구조
최대힙 구조
- 부모 노드의 값은 항상 자식 노드의 값보다 크다.
- 전체 트리의 Root 노드 값이 가장 크다.
최소힙 구조
- 자식 노드의 값은 항상 부모 노드의 값보다 크다.
- 전체 트리의 Root 노드 값이 가장 작다.
힙의 배열 저장 방식
- Root 노드는 배열의 첫 번째 A[1]에 저장
- 각각의 노드들은 레벨별로 저장
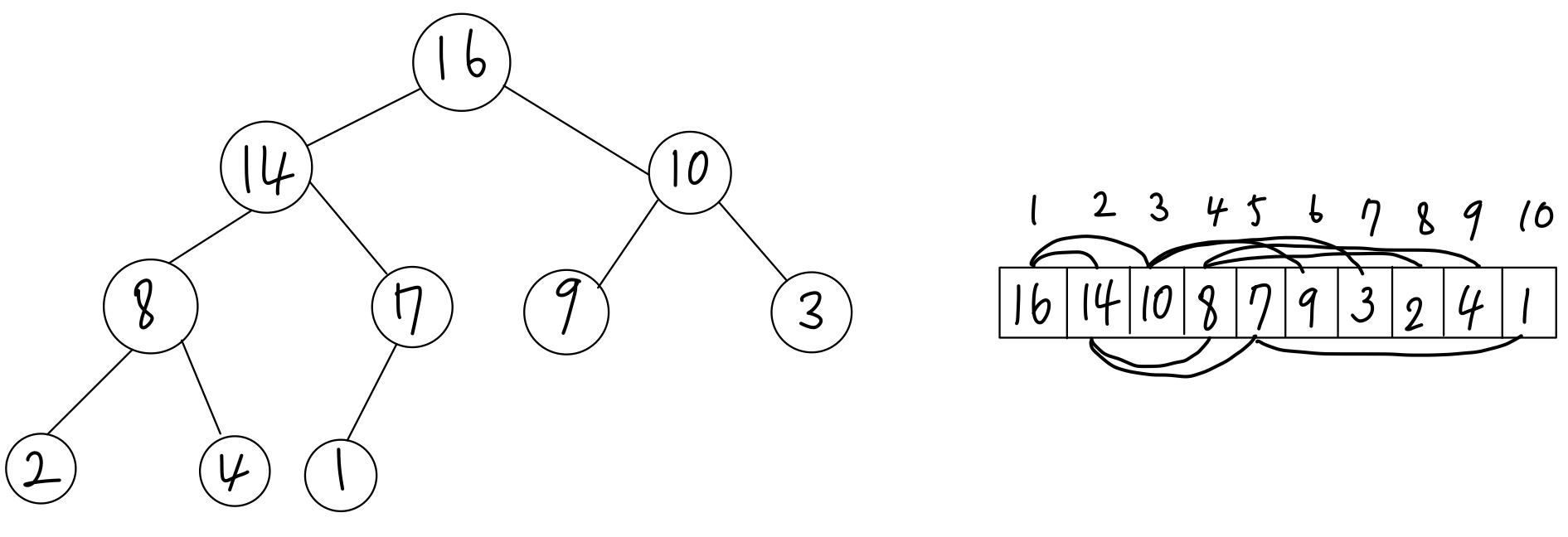
왼쪽은 개념인 것이고 실제 구현 형태는 오른쪽임
힙 구조
- 힙을 배열에 저장하면 다음과 같이 검색 가능
- Parent(i)
return [i/2]
- Left(i)
return 2i
- Right(i)
return 2i+1
힙의 높이
Root 노드로부터 트리의 높이
- Θ(lgn)
- Heap은 완전 이진 트리 구조를 가지기 때문에 각 레벨마다 노드의 수가 2배씩 증가하므로 높이는 Θ(lgn)

힙 구조 만들기
BUILD-MAX-HEAP(A)
A.heap-size = A.length
for i = [A.length / 2] downto 1
MAX-HEAPIFY(A,i)
처음 자식을 가지는 부모노드의 위치가 n/2라서 n/2부터 시작하는 것.
루트부터 시작하는 것이 아니라 아래에서부터 시작하는 것이 효율적.
힙 구조 만들기의 수행시간
수행시간 분석
- MAX-HEAPIFY를 한 번 호출할 때마다 O(lgn) => 이진트리라서
- MAX-HEAPIFY 호출 횟수는 O(n)
- 따라서 전체 수행시간은 O(nlgn)
'알고리즘' 카테고리의 다른 글
| [알고리즘]_알고리즘 문제해결 전략 3장 (0) | 2021.03.22 |
|---|---|
| [자료구조] ArrayList와 LinkedList (0) | 2021.03.15 |
| [알고리즘]_순환(Recursion)_3 반복문(Iteration)과 비교 (0) | 2021.01.29 |
| [알고리즘]_순환(Recursion)_2 순환의 적용 (0) | 2021.01.29 |
| [알고리즘]_순환(Recursion)_1 개념 및 예제 (0) | 2021.01.28 |